solution

Jobs arrive at rate γ in the system shown in Fig. 5.8. With probability
p, a customer is sent to queue 1, independently of the other jobs; otherwise, the job
is sent to queue 2. For i = 1, 2, queue i serves the jobs at rate μi . Find the value
of p that minimizes the average delay of jobs in the system. Compare the resulting
average delay to that of the system where the jobs are in one queue and join the
available server when they reach the head of the queue, and the fastest server if both
are idle, as shown in the bottom part of Fig. 5.8.
Hint The system of the top part of the figure is easy to analyze: with probability
p, a job faces the average delay 1/(μ1 − γp) in the top queue and with probability
1 −p the job faces the average delay 1/(μ2 −γ ( 1 −p)), One the finds the value of
p that minimizes the expected delay. For the system in the bottom part of the figure,
the state is n with n ≥ 2 when there are at least two jobs and the two servers are

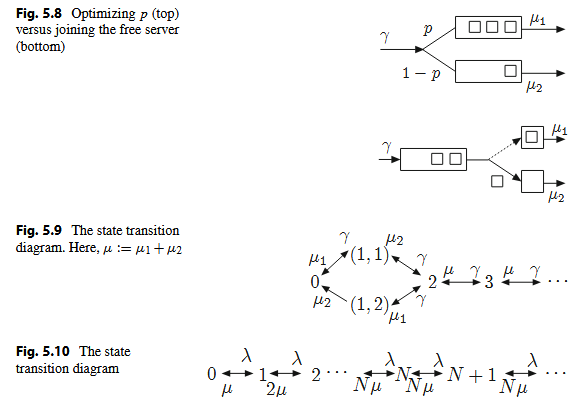
busy, or (1, s) where s ∈ { 1, 2} indicates which server is busy, or 0 when the system
is empty. One then needs to find the invariant distribution of the state, compute the
average number of jobs, and use Little’s Law to find the average delay. The state
transition diagram is shown in Fig. 5.9.