The N-Queens problem is a classic problem in computer science, due to its interesting computational behavior, depth-first searching and backtracking, and the fact that its processing time grows at a nonpolynomial (NP) rate. Thus, as the problem size grows, the execution time grows at a much more dramatic pace. Based on the chess game, there are numerous variations of the problem description. We ask you to develop a parallel UPC++ program that seeks to find all solutions to the problem of placing N queens on an N × N chessboard such that no queen can capture the other. As
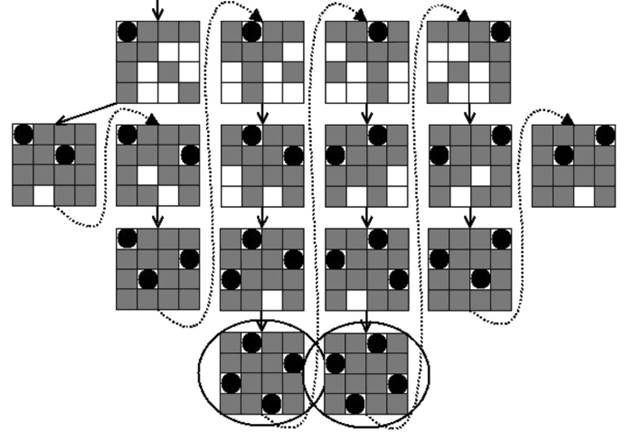
the queen is the most versatile chess piece and it can be moved in horizontal, vertical, and diagonal directions, this implies that no two queens can be placed on the same row, column, or along the same diagonal.Fig. 10.10 shows the computational flow in the N-Queens problem using a simple example of a 4 × 4 chessboard. The algorithm starts by placing the first queen in the first column of the first row, then shading all boxes along the same row, column, or diagonal. Then we attempt to placethe second queen in the second row in the first open position. It is clear after placing the second queen that no more queens can be placed on the board; therefore, this path was abandoned and we
had to backtrack to where a queen was placed in the second column of the first row. The algorithm continues, and at the end it is apparent that only two valid solutions, in which all four queens can be safely placed, exist. As the problem size increases, the number of iterations required to search for all possible ways
that the N-Queens can coexist on the same board grows dramatically. Luckily, N-Queens lends itself to parallelism. This is because N-Queens is a tree-search problem in which the subtrees are independent of one another and therefore can be distributed across a number of threads. Develop a parallel UPC++ program to solve the N-Queens problem for an arbitrary chessboard dimension (indicated through command line). Distribute the elements of the first row among the UPC++ threads so that each thread performs the sequential problem for the case where a queen has placed in the first row and the assigned columns. You should represent the constraints (gray
Â
squares) present in the current state. You can use a data structure to represent them in a binary format (0 for legal positions and 1 for illegal positions).
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"


