Consider the sequence of independent random variables X1, X2, X3, … having the uniform densities
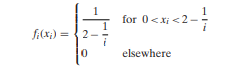
Use the sufficient condition of Exercise 7 to show that the central limit theorem holds.
Exercise 7
The following is a sufficient condition for the central limit theorem: If the random variables X1, X2, … , Xn are independent and uniformly bounded (that is, there exists a positive constant k such that the probability is zero that any one of the random variables Xi will take on a value greater than k or less than −k), then if the variance of
![]()
becomes infinite when n→q, the distribution of the standardized mean of the Xi approaches the standard normal distribution. Show that this sufficient condition holds for a sequence of independent random variables Xi having the respective probability distributions
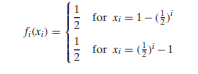
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"


